行星齿轮的特征频率

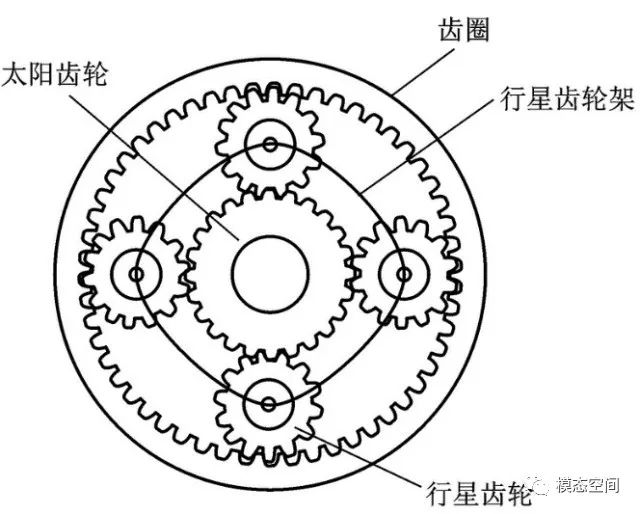
对于单排行星齿轮而言，行星轮与太阳轮啮合，还要与齿圈啮合。行星轮的轴线围绕太阳轮的固定轴旋转，支承行星轮作自转并带动行星轮作公转的行星架围绕太阳轮的轴线旋转，因此，行星齿轮系存在多个构件旋转，不像定轴齿轮只有一对齿轮幅旋转，故，相对于定轴齿轮而言，行星齿轮的特征频率更复杂。

单排行星齿轮可以任意固定齿圈、太阳轮和行星架中的任一个构件。如当固定齿圈时，太阳轮作为输入的主动轮，行星架作为输出的从动轮，此时齿轮箱可作为减速器。当固定太阳轮时，行星架作为输入的主动轮，齿圈作为输出的从动轮时，齿轮箱可作为增速器。固定行星架时，太阳轮作为输入的主动轮，齿圈作为输出的从动轮时也可视作减速器（因为齿圈的齿数通常多于太阳轮的齿数）。另外，这三个构件还可任一联锁其中两个构件，那么，此时则按1：1输入输出，即传动比为1。

在这，我们仅详细考虑第一种情况，即齿圈固定，太阳轮作为输入的主动轮，行星架作为输出的从动轮，因而，行星架的转速是输出轴的转速。假设齿圈、太阳轮和单个行星轮的齿数分别为z₁、z₂和z₃，行星轮的数量为n。行星齿轮各旋转部件的转动频率如下：

l  太阳轮相对于箱体的转频为f₀（输入转频）；

l  行星架相对于箱体的转频为f₁（输出转频）；

l  行星轮相对于行星架的转频为f_p。

由于行星齿轮旋转的构件包括太阳轮、行星轮和行星架，因此，计算各个构件的转频时相对复杂，如果行星齿轮的频率计算能按照定轴齿轮来计算，则简单得多，因此，我们要将行星齿轮转化为定轴齿轮来计算各个频率成分。转化之后，可视行星齿轮为定轴齿轮，因而计算各个频率成分则简单了。这个思路一直贯穿全文，这样在理解各个频率成分时也应按定轴齿轮来理解。

在这，将其他构件的转速（或转频）以行星架为参考，则可认为行星架固定不动，因此行星轮将不存在公转，只有自转，从而将行星齿轮转化为定轴齿轮来计算各个特征频率。此时，太阳轮相对于行星架的转频等于f₀-f₁，齿圈相对于行星架的转频等于-f₁。考虑到太阳轮与行星轮啮合，行星轮与齿圈的内齿啮合，此时，行星轮可视作中间轮，根据定轴齿轮的啮合特征，我们知道中间轮不会影响齿轮的啮合频率（参考《齿轮结构的频谱特征》一文），则齿轮的啮合频率如下（负号代表旋转方向相反）

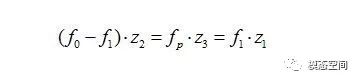
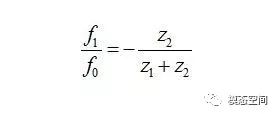
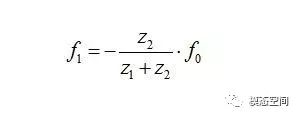
l  齿圈的任一个齿与行星轮的啮合频率f₂；

l  太阳轮的任一个齿与行星轮的啮合频率f₃；

l  行星轮的任一个齿与太阳轮或齿圈的啮合频率f₄。

齿圈相对于行星架的转频为f₁，由于行星轮的数量为n，则

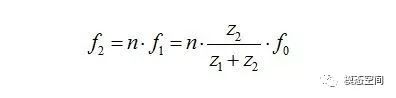
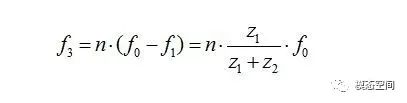
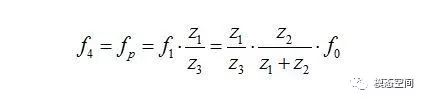
l  单个行星轮与齿圈的啮合频率f₅；

l  所有行星轮与齿圈的啮合频率f₆；

l  由于齿圈的齿距误差导致所有的行星轮驱动行星架的机械功率都不是均匀一致的，这将会导致单个行星轮出现有别于f₅的啮合频率f₇。

由于转化之后是按定轴齿轮来处理，因此，单个行星轮与齿圈的啮合频率也等于行星轮与太阳轮的啮合频率。根据定轴齿轮的啮合频率计算公式可知，单个行星轮与齿圈的啮合频率等于行星轮的转频乘以它的齿数，也等于齿圈的转频乘以齿圈的齿数，即

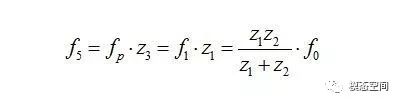
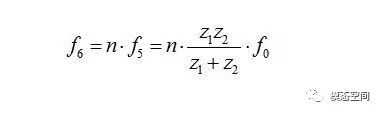
如果齿圈是完美的齿轮，即不存在齿距误差，那么，所有行星轮驱动行星架的机械功率是均匀一致的，各个行星轮的负载大小完全相同，不存在时大时小或者完全不受负载的情况。但生产出来的齿圈中的内齿或多或少存在局部齿距误差，从而导致单个行星轮驱动行星架的机械功率流的非均匀分布。某个行星齿轮接近局部的循环齿距误差时将传递全部机械功率，而其他的行星轮传递的功率将减少甚至不传递任何功率。当满载的行星轮通过一对带局部循环齿距误差的轮齿时，它将完全不承受任何负载。行星轮的全负荷运转对应于齿圈齿数除以行星轮数量，即z₁/n。啮合周期数目可能是一个整数，因此，它是分式z₁/n的整数部分。数学上这个取整数部分可以用[z₁/n]来表示。在行星架旋转完整一圈中，所有行星轮都连续成为负载最重的行星轮。在行星架旋转完整一圈过程中，总共有n*[z₁/n]个啮合周期。因此，啮合频率f₇计算如下

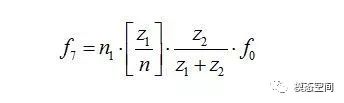
对于齿圈固定的单排行星齿轮，啮合频率计算公式如下：