似然与概率傻傻分不清楚？

→ 模型已知：公平骰子（每个点数的概率是 1/6）

→ 事件：掷出一个“6”

→ 概率：P(掷出6) = 1/6

H1：骰子是公平的；H2：骰子偏向 6（掷出6的概率是0.5）

→ 模型未知，数据已知：现在我们想知道哪个模型更可能“产生”这组结果。

→ 这是似然问题。

– 如果已知 θ，求 data 的概率 ⇒ 这是概率

– 如果已知 data，比较不同 θ 哪个更可能 ⇒ 这是似然

→ 如果你已经看到了水坑，想推断是下雨还是洒水 ⇒ 似然

似然 (Likelihood): 面向模型，用于估计参数，是反向推理（数据 ➝ 模型）

在所有可能的参数中，找到最有可能生成你观察到的数据的那一组。

用掷硬币举个简单例子

你怀疑一枚硬币可能不是公平的，于是你连续抛了10次，结果是：

正面：7 次，反面：3 次

你现在的问题是：这个硬币正面朝上的概率 p 是多少？

方法一：拍脑袋猜？

也许你想说，7/10 = 0.7，那 p=0.7 吧？

这其实就是最大似然估计给你的答案！

最大似然的数学想法

MLE 会问一个问题：

“如果硬币正面朝上的概率是某个值 p，那么看到 7 次正面、3 次反面的可能性有多大？”

这个可能性叫做“似然（Likelihood）”，我们可以写成：

L(p) = P(看到这个数据 | p) = C(10, 7) * p^7 * (1-p)^3

你会发现，这个式子在 p = 0.7 时取得最大值。也就是说：在所有可能的 p 值中，p = 0.7 最有可能生成我们观察到的结果。

图像理解：谁的“解释力”最强？

我们可以把似然函数画出来：横轴是不同的 p 值，纵轴是“看到这组数据”的可能性。

你会发现图像在 p = 0.7 处达到峰值。这一点，就是最大似然估计给出的答案。

见下图：

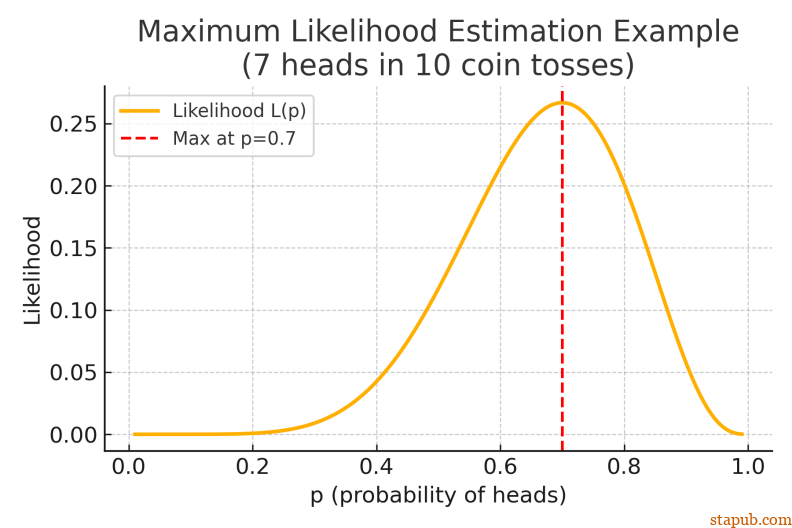
最大似然估计 的作用就是：找出那个“最符合现场数据”的嫌疑人。

– 逻辑回归 / 线性回归

– 高斯混合模型

– 隐马尔可夫模型（HMM）

– 深度学习中的交叉熵损失

和贝叶斯方法的区别？

MLE 是只关心“哪个参数最有可能解释数据”，它不考虑先验知识。

而贝叶斯方法会说：

“我有点先验知识，再结合你给我的数据，一起算出‘后验’。”

方法比较：

– 最大似然 MLE：不考虑先验，输出最可能的参数点估计

– 贝叶斯估计：考虑先验，输出参数的概率分布（后验）