共计 1848 个字符,预计需要花费 5 分钟才能阅读完成。
一、前言
疲劳分析通常是在时域进行,所有的输入载荷和输出应力都是基于时间的信号。时域疲劳可以通过静应力分析或者模态瞬态法进行分析,其中模态瞬态法一般用于需要考虑共振对疲劳的影响,载荷的加载频率接近系统的共振频率。在一些情况下,共振应力和输入载荷却通过频域信号来分析,通常用PSD功率谱密度来表达,基于的PSD频域疲劳预测方法比时域疲劳预测方法有以下优势:
- 时域所得损伤是取自对一段随机变化信号的计数,因此通过时域方法获得的损伤本身就是一个随机变量,无法避免对所得的损伤结果进行统计推断。通常,用雨流计数法得到的零部件应力幅值服从威布尔分布,均值服从正态分布。这些需要进行循环计数,数据处理量非常大。而基于PSD的频域分析方法计算简单,不需要循环计数。
- 随机动态应力,在时域内需要很长的信号记录才能准确地描述随机响应,同时处理长的时域信号非常困难,而得到频域功率谱应力信号则较为方便。
- 用来进行疲劳分析的频域信号采样率,只要达到时域信号采样率的1/10就可以得到与用时域信号预测同样精度的结果,频域信号的读取、储存都比时域信号方便。
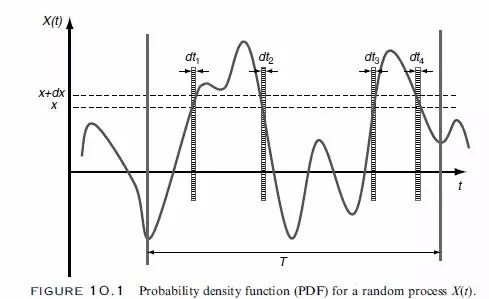
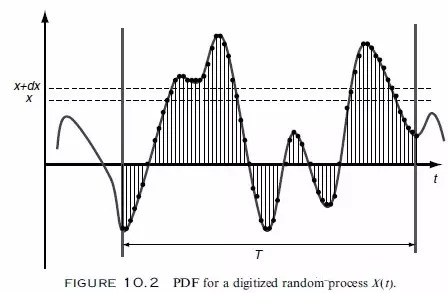
当系统所受到的载荷信号是随机不确定的时候,我们通常采用随机振动分析的进行疲劳分析。假设所受载荷X(t)在x 和x+dx 范围内,在一个总时长T 的时间段内,载荷出现的概率为fx(x)。
图1
如果T 足够长,fx(x) 可以通过下式表达:
相对的概率密度函数PDF可以通过总的时间段在带宽X 和X+dX 段,如图2所示
图2
随机信号X(t) 的均值和均方根值可以表示为:
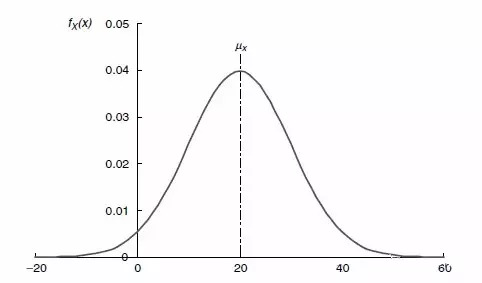
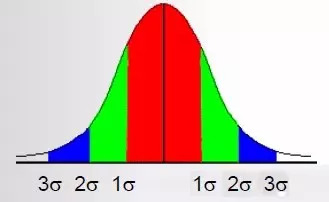
这里T 是总的时长,当ux=0时,就是随机信号X(t) 的均方根RMS Fx(x)服从高斯正态分布
图3
图4
因为随机振动激励被假设为服从高斯正态分布,各幅值发生概率为:
图5
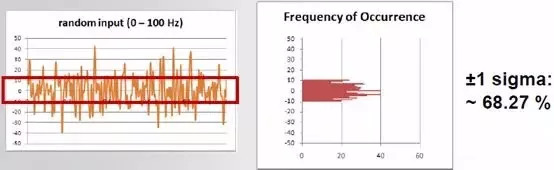
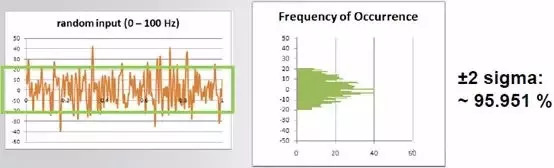
基于这个特点,在实际计算中一般取3 sigma为计算的上限。高斯正态分布具有以下重要属性:如果高级正态分布激励作用在线性系统上,则输出的激励是不同的随机过程,但是仍然服从另外一个高斯正态分布。
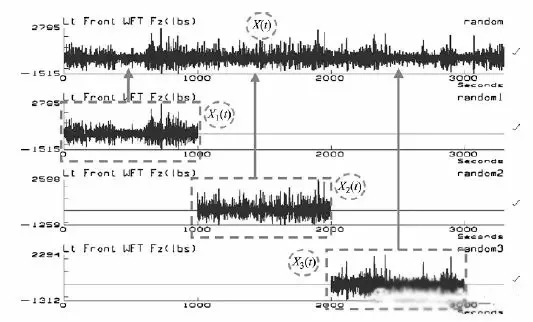
举个随机信号的处理过程的例子:
图6
图7
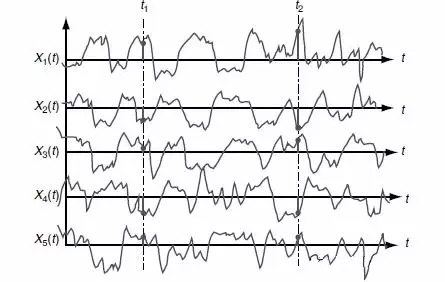
信号X(t) 被分解为几段,如图6和图7所示,对于平稳的随机过程x(t) ,时间历程是非周期的,因此不能用傅里叶级数表示;而且x(t)是一个无限长的信号,不能通过傅里叶变换得到该随机过程的频域信息。这个困难可以通过对该随机过程的自相关函数Rx(τ) 做傅里叶变换来解决。
由于X(t) 是平稳随机信号其均值和标准差是独立于时间t 的,因此
相关系数
如果对随机过程x(t) 的零点进行处理,使得该过程的平均值为0,并且假定x(t) 不含有周期性分量,那么Rx(τ∞)=0,条件得到满足。我们就可以得到自相关函数的Rx(τ) 傅里叶变换和逆变换。
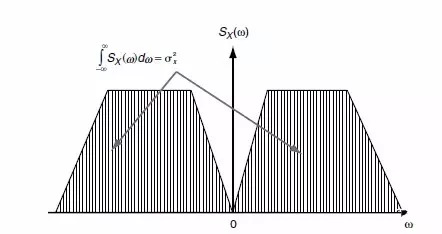
其中函数Sx(ω) 称为功率谱密度。我们令τ 为0,则得到:
图8
这是Sx(ω) 最重要的一个特性,即功率谱密度曲线下的面积就是平稳随机过程x(t) 的均方值,所以函数Sx(ω) 又叫均方谱密度,其单位是(x的单位)²/(rad/s),常见的有加速度随机激励单位为(mm/s²)2/Hz或G2/Hz。速度随机激励单位为(mm/s)²/Hz ;位移随机激励单位为(mm)²/Hz。
在上面的推导过程中,圆频率ω 取值是从负无穷到正无穷,但我们研究振动更习惯用频率f而不是圆频率ω,频率f 的取值应该是从0到正无穷,单位应该是Hz而不是rad/s。所以双侧谱密度Sx(ω) 可以变换为一个等效的单侧谱密度。
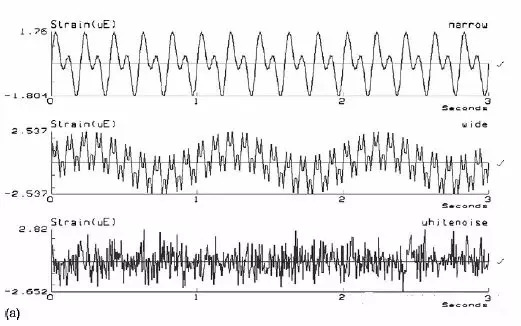
图9 依次为窄带、宽带、白噪声信号
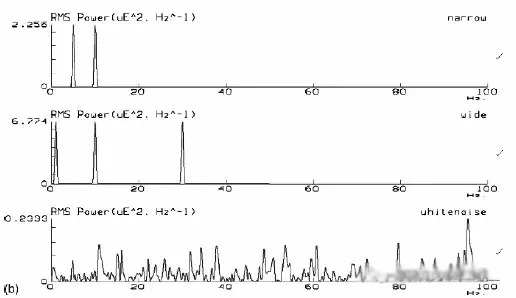
图10 依次为其频谱图
窄带随机过程的时间历程类似于振幅和相位随机变化的正弦波。根据窄带随机过程的PSD曲线,我们可以得到它的很多特性,如频率成分和有效值等,还可以进一步得到其峰值分布的信息,即组成这个过程的一系列正弦波的幅值分布信息。也就是说,我们可以依据应力PSD曲线求得时间段T内的应力循环次数,以及应力幅值在S 和S+dS 之间的概率Pp(S)dS 。由PSD求得应力循环次数v 和应力幅值区间概率Pp(S)dS 的公式推导比较复杂,建议读者参考《随机振动与谱分析概论》一书,本文不再介绍。
对于宽带随机过程,以上述窄带分析法为基础进行拓展,也可得出计算疲劳损伤的近似表达式。常见的宽带疲劳算法有DirliK算法、Wirsching-Light算法等,其中Dirlik算法的计算结果与试验结果接近,成为基于功率谱密度计算疲劳失效的首选算法,已被大多数商用疲劳分析软件采用。
来源:易萌森戈CAE工作室公众号(ID:EMSGCAE),作者:黄森。

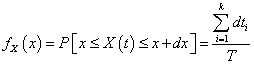
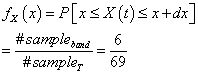
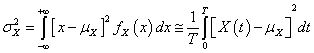
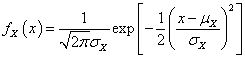









 大师兄
独立事件和卡方检验,都是非常重要的质量管理概念,挺难理解的。
大师兄
独立事件和卡方检验,都是非常重要的质量管理概念,挺难理解的。