SPC八大判异规则 适用每一种控制图吗？

共计 1529 个字符，预计需要花费 4 分钟才能阅读完成。

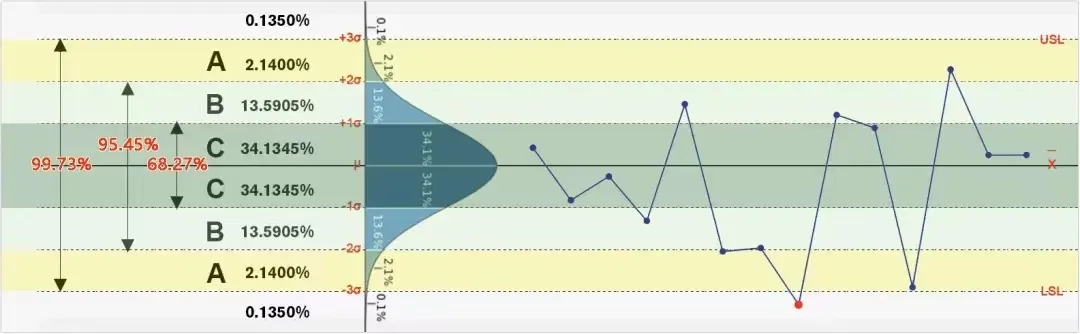
我们把八大判异规则分成两类

普遍适用的规则（核心规则）：

• 规则1：一个点超出控制限（±3σ）。

• 规则4：连续7个点落在中心线同一侧。

• 规则5：连续6个点持续上升或下降。

• 规则7：连续15个点落在C区（中心线上下1σ以内）。

依赖分布的规则（需谨慎适用）：

• 规则2：连续3个点中的2个落在A区或者A区之外（中心线±2σ之外）。
• 规则3：连续5个点中的4个落在B区或B区之外（中心线±1σ之外）。
• 规则6：连续8个点落在中心线两侧的C区以外（中心线±1σ以内）。
• 规则8：连续14个点交替上升和下降。

1. 单值控制图（I图）

适用性：核心规则和依赖分布的规则通常都适用 。

原因：I图假设数据服从正态分布或近似正态分布 ，因此基于中心线和标准差区域的所有八大规则都能够有效捕捉过程的异常。

2. 单值移动极差控制图（MR图）

适用性：通常只适用核心规则。

原因：MR图监控的是连续观测值之间的差值，其分布通常不是正态分布 。核心规则中的规则1检测变异性的异常跳跃，规则4、规则5和规则7可以识别短期变异中的持续偏差或趋势。

3. 均值控制图（X-bar图）

适用性：核心规则和依赖分布的规则通常都适用 。

原因：根据中心极限定理 ，当子组样本量足够大时，子组均值的抽样分布趋近于正态分布 。因此，基于正态分布制定的所有八大判异规则都适用于监控子组均值的X-bar图。

4. 极差控制图（R图）

适用性：通常只适用核心规则。   

原因：子组极差的分布不是正态分布 。核心规则中的规则1检测变异性的异常跳跃，规则4、规则5和规则7可以识别短期变异中的持续偏差或趋势。     

5. 标准差控制图（S图）

适用性：通常只适用核心规则。   

原因：子组标准差的分布也不是正态分布 。与极差类似，核心规则中的规则1检测变异性的异常跳跃，规则4、规则5和规则7可以识别短期变异中的持续偏差或趋势。    

6. 均值移动极差控制图（X-bar MR图）

适用性：类似于单值移动极差图，移动极差图部分通常只适用核心规则。

原因：与极差类似，核心规则中的规则1检测变异性的异常跳跃，规则4、规则5和规则7可以识别短期变异中的持续偏差或趋势。  

7. 不合格品数控制图（np图）

适用性：通常只适用核心规则。   

原因：np图监控的数据服从二项分布 。二项分布在极端比例下可能不对称。核心规则通常适用。其他规则不通用。

8. 缺陷数控制图（c图）

适用性：通常适用核心规则。

原因：c图监控的数据服从泊松分布 。泊松分布通常不对称，尤其是在均值较小时。核心规则通常适用。

9. 不合格品率控制图（p图）

适用性：通常适用核心规则中的规则。

原因：p图监控的数据服从二项分布 。与np图类似，由于二项分布的特性和样本大小变化可能影响控制限，规则2和规则3的应用需要谨慎。核心规则通常适用。

10. 单位缺陷数控制图（u图）

适用性：通常适用核心规则中的规则。

原因：u图监控的数据服从泊松分布 ，且控制限随样本大小变化。这使得直接应用依赖分布的规则变得不切实际。核心规则通常适用。