共计 1959 个字符,预计需要花费 5 分钟才能阅读完成。
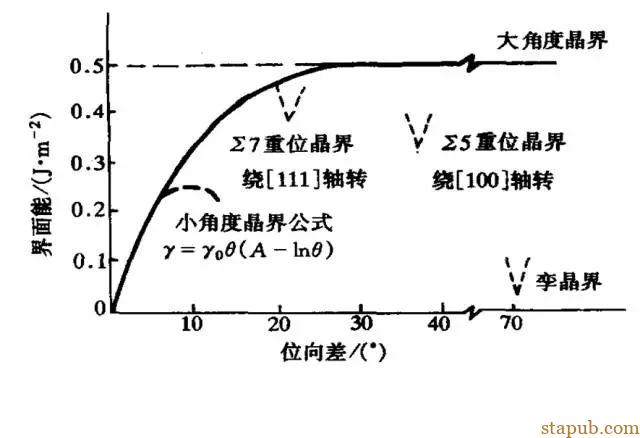
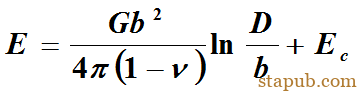 式中G剪切模量,b柏氏矢量,ν泊松比,Ec位错中心能量,D位错间距。2.大角晶界能(1).任意大角晶界能(2).特殊大角晶界能:a.共格孪晶界:是一种有孪晶关系的对称倾转晶界。共格原子基本处于无畸变的状态,共格孪晶界的能量非常低。b.非共格孪晶界:非共格态导致界面能较高。3.晶界的能量
式中G剪切模量,b柏氏矢量,ν泊松比,Ec位错中心能量,D位错间距。2.大角晶界能(1).任意大角晶界能(2).特殊大角晶界能:a.共格孪晶界:是一种有孪晶关系的对称倾转晶界。共格原子基本处于无畸变的状态,共格孪晶界的能量非常低。b.非共格孪晶界:非共格态导致界面能较高。3.晶界的能量
二、晶界平衡偏析
1. 晶界偏析:在平衡条件下,溶质原子(离子)在晶界处浓度偏离平均浓度。
(1).偏析的自发趋势:晶界结构缺陷比晶内多,溶质原子(离子)处于晶内的能量比处在晶界的能量高,通过偏析使系统能量降低。
(2).偏析驱动力是内能差:设一个原子位于晶内和晶界的内能分别为El和Eg,则偏析的驱动力为:
(3).偏析阻力是组态熵(结构熵):溶质原子趋向于混乱分布,晶内位置数(N)大于晶界位置数(n),构成了偏析的阻力。设晶内及晶界的溶质原子数分别为P和Q,则P个溶质原子占据N个位置和Q个溶质原子占据n个位置的组态熵为:
(4).偏析表达式该分布状态下的吉布斯自由能为(斯特林公式lnx!≈xlnx-x):
平衡条件为:
平衡关系式:
或:
用C及C0表示晶界和晶内的溶质浓度,则:
令ΔE表示1mol原子溶质位于晶内及晶界的内能差:
对稀固溶体,C0<<l,上式近似写成:
再做近似:
(5).影响晶界偏析的因素
●溶质浓度C0: 随溶质的平衡浓度增加而增加。
●温度:因△E为正,故随温度升高C下降。温度高TS项影响大,使偏析的趋势下降;但温度过低,平衡C虽高,但受扩散限制而达不到较高的C值。
●内能△E:内能差△E越大,偏析浓度C越高。内能差与溶质和溶剂原子尺寸差相关,也与电子因素有关。
●界面能变化:能降低界面能的元素,易形成晶界偏析。根据等温吸附方程:
三、晶界迁移
1.晶界迁移速度
考虑两晶粒组成的界面,两晶粒的化学位为μⅠ>μⅡ,作用于原子的力是吉布斯化学位梯度-dμ/dz。于是当界面厚度为λ,则晶粒I的一界面原子
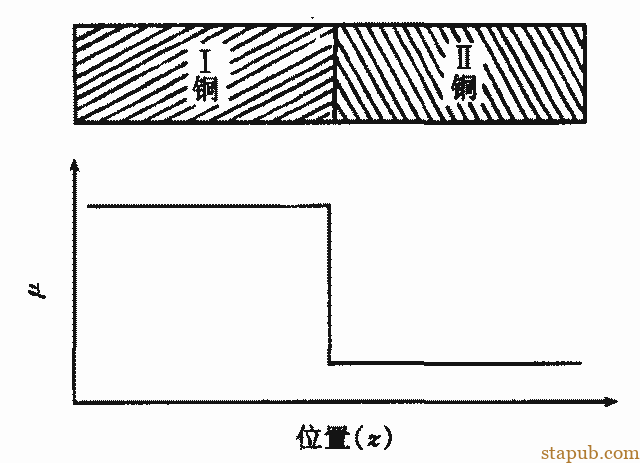
受到的力:
晶界迁移速度取决于晶界两侧的化学位差和晶界原子的迁移率。
2.界面迁移驱动力
两个驱动力:晶界曲率产生的化学位差和形变能。
a.界面曲率
附加压力的拉普拉斯公式:
对半径为r的球形曲面:
热力学等温条件下有:
Vm为摩尔体积。如取界面两侧Vm为常数,积分得到球状界面两侧的化学位差为:
凸侧的化学位高,晶界移动总是向着曲率中心移动。
b.形变能晶粒变形不同,缺陷密度不同,导致吉布斯自由能不同。设一双晶体,其中晶粒I变形小,因吉布斯化学位u于偏摩尔自由能G,其间化学位差:
忽略体积项与熵项,得到:
令晶粒I的形变能为零,可得:
NA为阿伏加德罗常数;ES为晶粒Ⅱ的摩尔形变能。说明:晶界的迁移速度随形变能的大小呈性线变化。
3.影响晶界迁移的主要因素
● 溶质原子:降低迁移率,与晶界偏析、晶界结构有关。
● 晶界第二相颗粒:阻碍作用,晶界脱离第二相颗粒的迁移是系统能量提高的过程(需生长出这段晶界),产生晶界迁移的阻力。
●温度 :迁移率与晶界扩散系数D 由Einstein 关系联系:
由上式知随温度的升高,晶界迁移率提高。
● 晶粒位向–晶界的晶粒取向差小,迁移率低。
四、界面能与显微组织形貌
1.复相中的第二相
晶内第二相第二相与基体的总界面能为∑Aiγi,引起的弹性应变能为ΔGS,平衡条件为:∑Aiγi+ΔGS= 最小实际析体形状取决于表面能和应变能两因素的强弱。
●表面能最小,析出等轴状。
●应变能最低,析出薄片状或盘状。
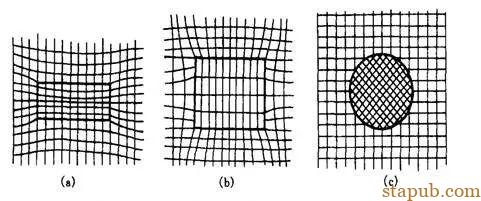
●共格和半共格析出:共格界面的匹配使应变能最小占优,易析出片、盘或针状。
●非共格析出:无切应变,但出现热膨胀不同的正应力。
(a)共格 (b)半共格 (c)非共格
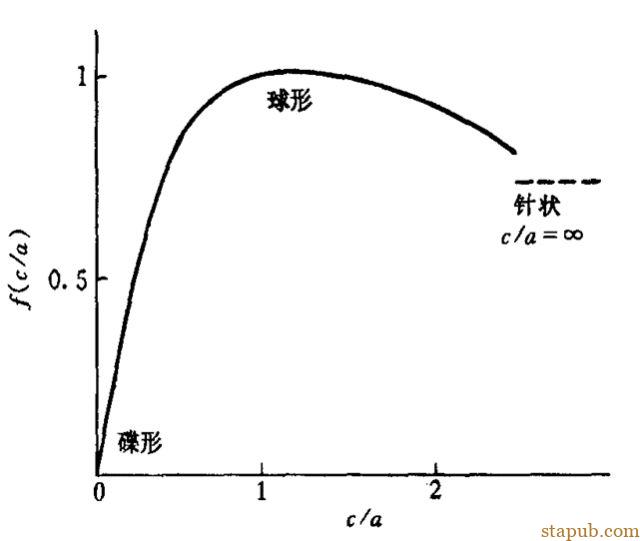
分析右图:球状(c/a= 1)的应变能最高,蝶状(c/a→0)的很低,针状(c/a→∞)的在二者之间。若一非共格析体的平衡形状是椭球,则表明界面能和应变能的共同作用决定了椭球的c/a值。当Δ很小,界面能起主要作用,析体将更近似于球状。
弹性应变能相对值与(c/a)的关系
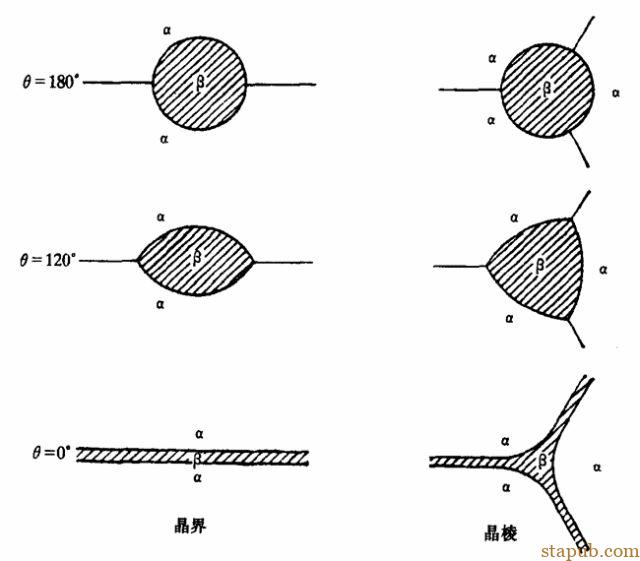
2.晶界第二相第二相(β)存在于基体(α)的晶界时,第二相在两基体晶粒间张开的角θ称二面角。平衡条件下,有如下关系:
γαα为α相间的界面张力;γαβ为α相和β相之间的界面张力。
3.二面角的界面张力平衡
θ的大小与第二相形貌:
θ取决于界面张力的比值γαα/γαβ。
●γαα<<γαβ,θ=180°,β与α完全不浸润,β近似球形;
●γαα= γαβ,θ= 120°,β呈双球冠形;
●γαα= 2γαβ,θ= 0°,β与α浸润,β在α晶界上铺展。

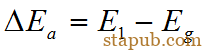
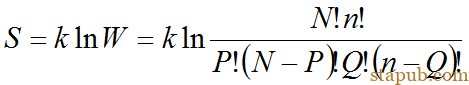
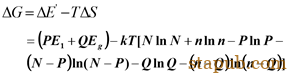
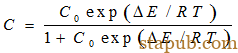
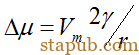
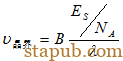









 大师兄
独立事件和卡方检验,都是非常重要的质量管理概念,挺难理解的。
大师兄
独立事件和卡方检验,都是非常重要的质量管理概念,挺难理解的。